进化树构建之邻接法(Neighbor-Joining)的介绍
进化树构建
进化树构建的问题是推断可能产生给定基因序列数据的进化树的拓扑结构和分支长度。推断树中叶节点的数量应等于给定数据中基因序列的数量。
Neighbor-Joining Algorithm
Neighbor-Joining (NJ)树推理方法最初是由 Saitou 和 Nei 于 1987 年编写的。
它属于一类基于距离的方法用于构建进化树。 NJ 方法采用给定序列之间的成对进化距离矩阵来构建进化树。Neighbor-Joining是一种bottom-up 的聚类方法,常被用于系统发育树 (phylogenetic tree) 的构建当中。
成对距离通常从序列比对算法中获得,例如 Smith-Waterman 和 BLAST ,它们将每个基因序列与每个其他基因序列进行比对。比对得分可用作序列之间进化距离的估计。
可用于计算距离的程序包括:用于 DNA MSA 的 DNADIST 和用于 Protein MSA 的 PROTDIST 。这些程序是 PHYLIP 包的一部分。
我们得到的输出是一棵树以及分支长度
01
使用基于23种遗传信息的邻接法构建的18个人类群体的遗传距离图。 由日本国立遗传学研究所教授 Saitou Naruya 于 2002 年制作。
在每个阶段,树的两个最近的节点被选择并定义为我们树中的“邻居( neighbors )”。 邻居被定义为一对 OTU(Operational taxonomic units) ,它们有一个节点连接它们,其中 OTU为分类单元,换句话说是树的节点。 操作次数与 n3 成正比,其中 n 是序列数。
例子
使用 Neighbor Joining Algorithm 构建一个进化树。 我们将使用 n=6 个分类群的假设距离矩阵。
| A | B | C | D | E | |
|---|---|---|---|---|---|
| B | 5 | ||||
| C | 4 | 7 | |||
| D | 7 | 10 | 7 | ||
| E | 6 | 9 | 6 | 5 | |
| F | 8 | 11 | 8 | 9 | 8 |
- 计算每个分类群与所有其他分类群的净分化距离r
1 | r(i) = total distance of taxa i from all other taxa's |
| A | B | C | D | E | |
|---|---|---|---|---|---|
| B | 5 | ||||
| C | 4 | 7 | |||
| D | 7 | 10 | 7 | ||
| E | 6 | 9 | 6 | 5 | |
| F | 8 | 11 | 8 | 9 | 8 |
eg:
r(D) = 7 + 10 + 7 + 5 + 9 = 41
1 | r(A) = 5 + 4 + 7 + 6 + 8 = 30 |
- 使用以下公式为每对分类群计算新的距离矩阵 (M):
1 | M(i,j) = d(i,j) – (r(i) + r(j))/(n - 2) |
- M(A, B) 的计算示例
1 | M(A,B) = d(A,B) – (r(A) + r(B))/(n - 2) |
计算完的结果如下图
| A | B | C | D | E | |
|---|---|---|---|---|---|
| B | -13 | ||||
| C | -11.5 | -11.5 | |||
| D | -10 | -10 | |||
| E | -10 | -10 | -10.5 | -13 | |
| F | -10.5 | -10.5 | -11 | -11.5 | -11.5 |
- 使用这个新矩阵找到最接近的分类群 i, j 。考虑最小距离并将 u 指定为该对的连接节点。然后使用公式计算分支长度
1 | S(i,u) = d(i,j)/2 + (r(i)-r(j))/2(n-2) |
例子: 根据矩阵 M,最接近的分类群对是:AB = -13。从 U 到 A 和 U 到 B 的距离计算如下:
1 | S(A,U) = d(A,B)/2 + (r(A)-r(B))/2(n-2) |
- 计算从 U 到所有其他分类群的新距离。 u 和分类群 k 之间的距离 d(u, k) 由下式给出
1 | d(u,k) = [d(i,k) + d(j,k) - d(i,j)]/2 |
1 | d(U,C) = [d(A,C) + d(B,C) - d(A,B)]/2 |
其他距离保持原样。因此,新的矩阵距离矩阵将是:
| U | C | D | E | |
|---|---|---|---|---|
| C | 3 | |||
| D | 6 | 7 | ||
| E | 5 | 6 | 5 | |
| F | 7 | 8 | 9 | 8 |
在每一轮中使用新的距离矩阵重复步骤 1 到 4。 在递归地完成每一步之后,得到最终结果:
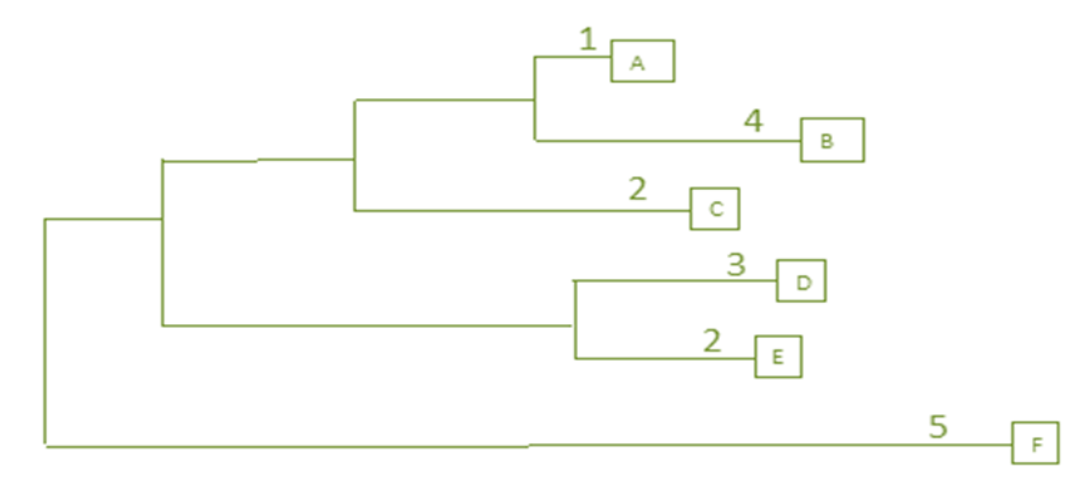
优缺点
好处:
-
它的计算速度很快,因此可用于大型数据集。
-
它不假设所有谱系都以相同的速度进化,即分子钟假设。
-
它不要求也不假定距离数据是超度量或可加的。
缺点:
它通常为某些分支分配负长度。
尽管一些实现尝试了“最小进化法( minimal evolution )”,但缺乏明确的最优性标准。








